Chapter 14 Heights and Distances
Class 10th R. S. Aggarwal Maths Solution
CBSE Class 10 Maths
R. S. Aggarwal Solution
Heights and Distances Exercise Ex. 14
Solution 1
Let AB be the tower
standing on a level ground and O be the position of the observer. Then OA = 20
m and ![]() OAB = 90° and
OAB = 90° and ![]() AOB = 60°
AOB = 60°
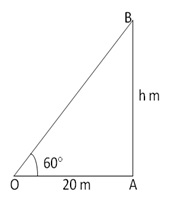
Let AB = h meters
From the right
![]() OAB, we have
OAB, we have
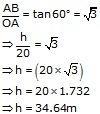
Hence the height of the
tower is ![]()
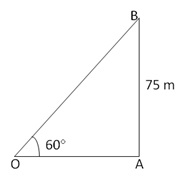
Solution 2
Let OB be the length of
the string from the level of ground and O be the point of the observer, then,
AB = 75m and ![]() OAB = 90° and
OAB = 90° and ![]() AOB = 60°, let OB = l meters.
AOB = 60°, let OB = l meters.
From the right
![]() OAB, we have
OAB, we have
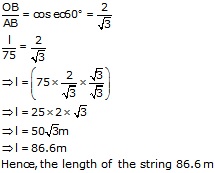
Solution 3
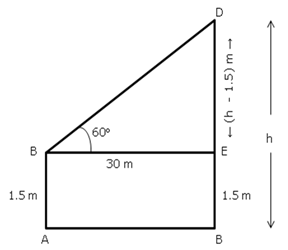

Solution 4

Solution 5
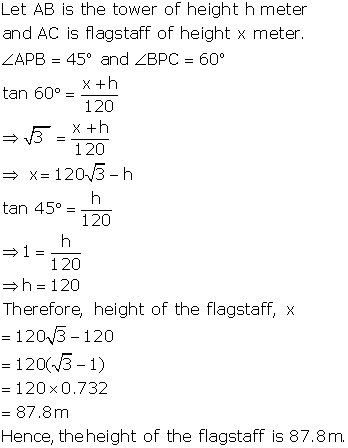
Solution 6

Solution 7
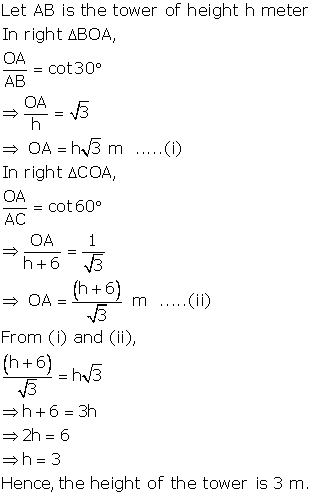
Solution 8
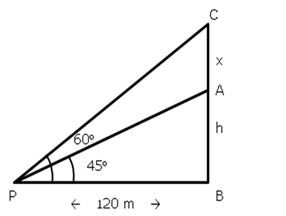
Let SP be the statue and PB be the pedestal. Angles of elevation of S and P are 60° and 45° respectively.
Further suppose AB = x m, PB = h m
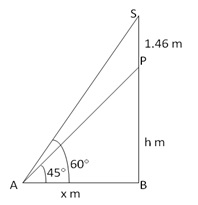
In right ![]() ABS,
ABS,
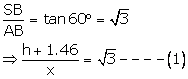
In right ![]() PAB,
PAB,

Thus, height of the pedestal =
2m
Solution 9
Let AB be the unfinished tower and let AC be complete tower.
Let O be the point of observation. Then,
OA = 75 m
![]() AOB
= 30° and
AOB
= 30° and
![]() AOC
= 60°
AOC
= 60°
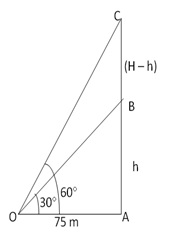
Let AB = h meters
And AC = H meters
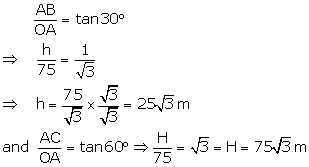
Hence, the required height is ![]()
Solution 10
Let AB be the tower and BC be flagpole, Let O be the point of observation.
Then, OA = 9 m, ![]() AOB
= 30° and
AOB
= 30° and
![]() AOC
= 60°
AOC
= 60°
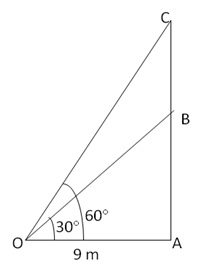
From right angled ![]() BOA
BOA
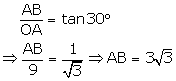
From right angled ![]() OAC
OAC

Thus ![]()
Hence, height of the tower= 5.196 m and the height of the flagpole = 10.392 m
Solution 11
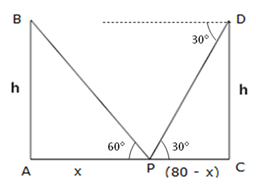
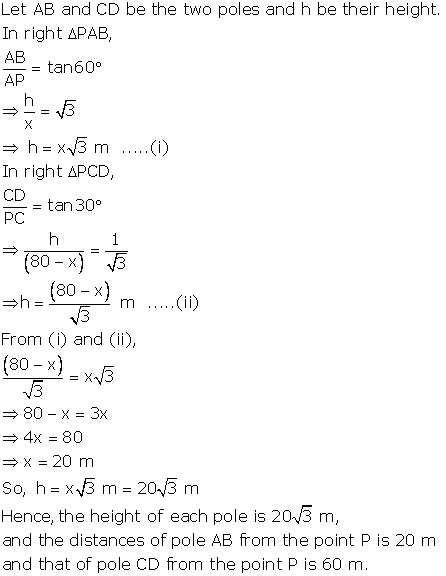
Solution 12
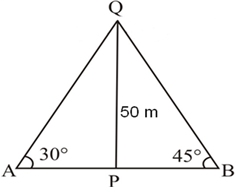

Solution 13
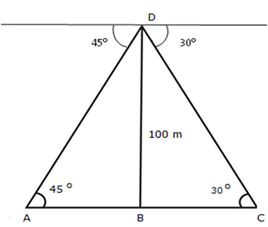

Solution 14
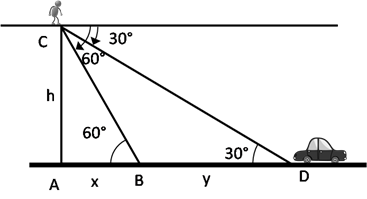

Solution 15
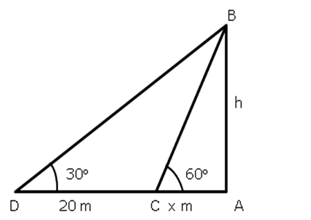

Solution 16
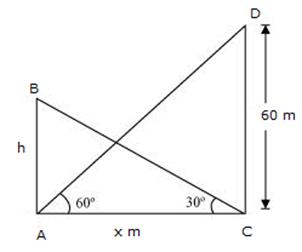
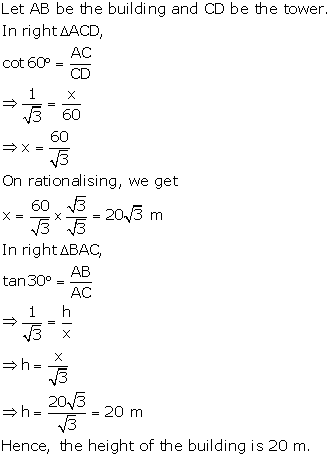
Solution 17
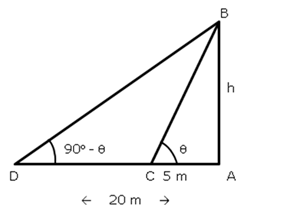
Let AB and CD be the first and second towers respectively.
Then, CD = 90 m and AC = 60 m.
Let DE be the horizontal line through D.
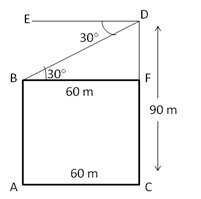
Draw BF ![]() CD,
CD,
Then, BF = AC = 60 m
![]() FBD
=
FBD
= ![]() EDB
= 30°
EDB
= 30°

Solution 18
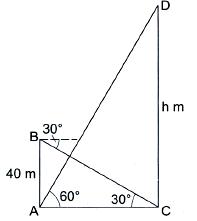

Solution 19
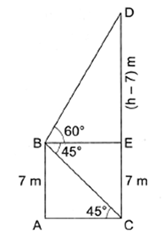

Solution 20
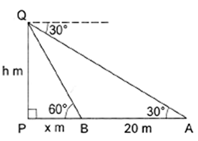

Solution 21
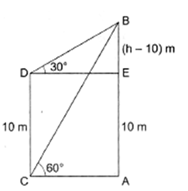

Solution 22
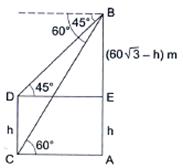

Solution 23
Let AB be the height of the deck and let CD be the cliff..
Let the man be at B, then, AB= 16 m
Let BE ![]() CD
and AE
CD
and AE ![]() CD
CD
Then, ![]() EBD
= 60 and
EBD
= 60 and ![]() EBC
= 30
EBC
= 30
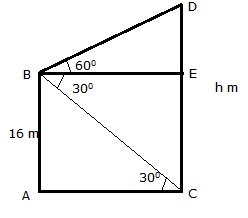
CE = AB = 16m
Let CD = h meters
Then, ED = (h 16)m
From right ![]() BED,
we have
BED,
we have
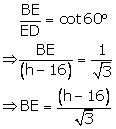
From right ![]() CAB,
we have
CAB,
we have

Hence the height of cliff is 64 m and the distance between the cliff
and the ship = ![]()
Solution 24
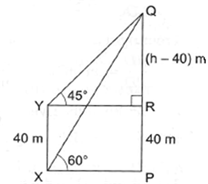
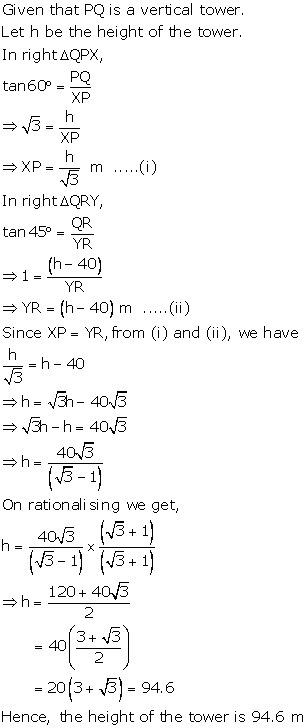
Solution 25

Solution 26
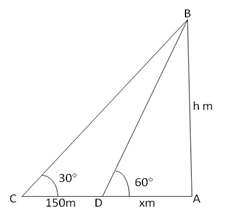
Let AB be the tower and let the angle of elevation of its top at C be 30°. Let D be a point at a distance 150 m from C such that the angle of elevation of the top of tower at D is 60°.
Let h m be the height of the tower and AD = x m
In ![]() CAB,
we have
CAB,
we have
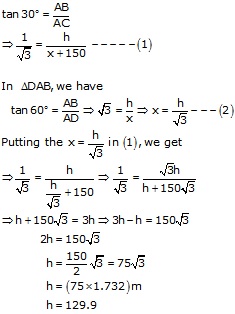
Hence the height of tower is 129.9 m
Solution 27
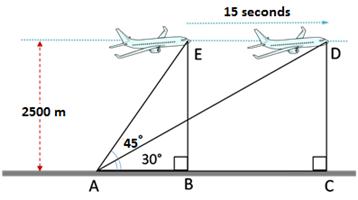
Let AB be the light house and let C and D be the positions of the ship.
Llet AD =x, CD = y
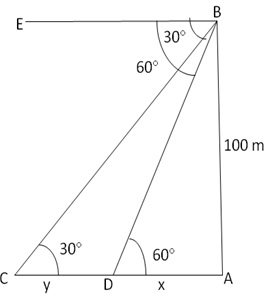
In ![]() BDA,
BDA,

The distance travelled by the ship during the period of observation = 115.46 m
Solution 28
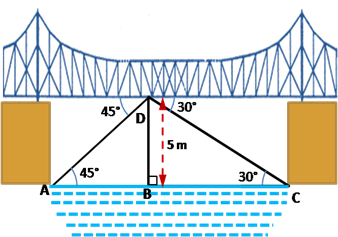

Solution 29
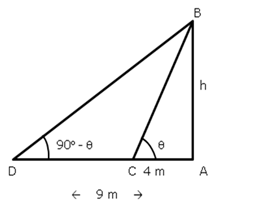

Solution 30
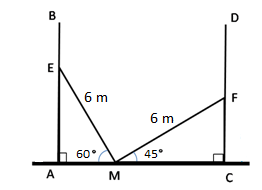

Solution 31
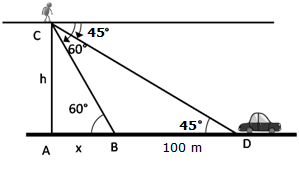

Solution 32
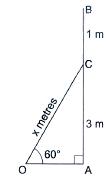
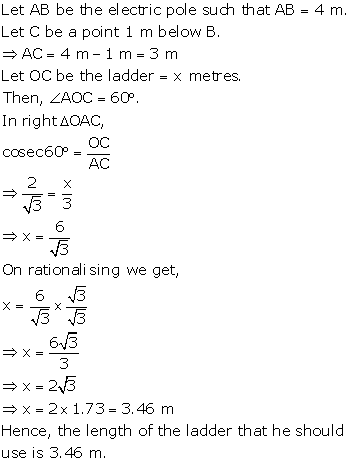
Solution 33
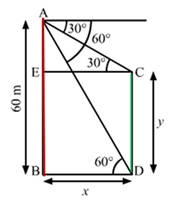

Solution 34
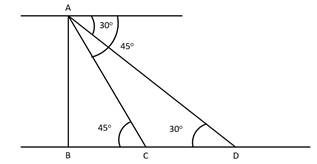
Let AB be the tower, and car moves from point D to C.
Now, we have
In ΔABC
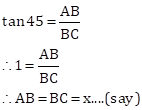
Also, we have
In ΔABD
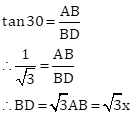
Now,

Solution 35
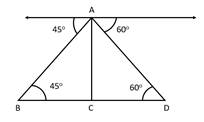
Let A be the aero plane,
BD be the river
AC is the perpendicular height = 300m
Now, we have
In ΔABC
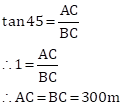
Also, we have
In ΔADC
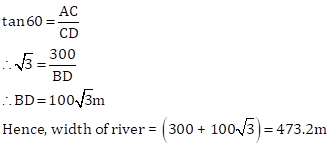
Solution 36
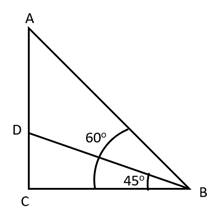
Let AD be the tower,
B be the point on ground,
CD will be the building.
Now, we have
In ΔBCD
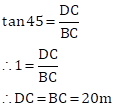
Also, we have
In ΔABC
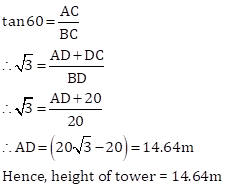
Solution 37
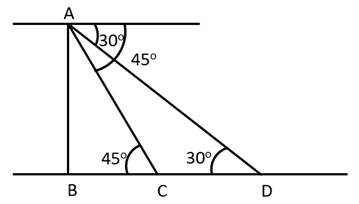
AB is the hill
C and D are the position of kilometer stones
Now, we have
In ΔABC
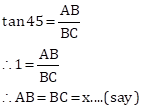
Also, we have
In ΔABD
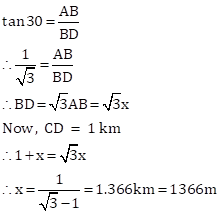
Hence, height of hill is 1366m.
Solution 38
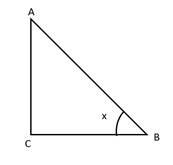
Let,
AC is the height of pole
BC is the shadow
In ΔABC
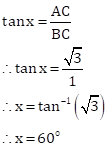
The angle of elevation of the sun is 60o.
Solution 39
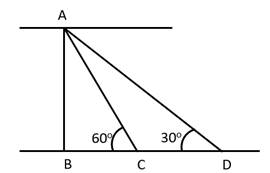
AB is the tower
C and D are positions of boat
Now, we have
In ΔABC
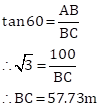
Also, we have
In ΔABD
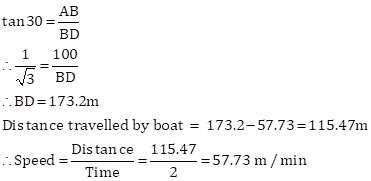
Hence the speed of the boat is 57.73 m/min.
Solution 40
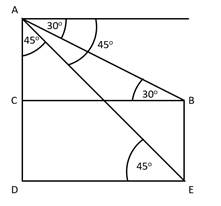
AD be the multistoried building
BE be the small building
Now, we have
In ΔADE
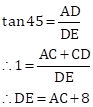
Also, we have
In ΔABC
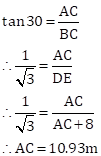
Hence the height of the multistoried building = 10.93+8 = 18.928 m
And the distance between both buildings is also 18.928 m
Heights and Distances Exercise MCQ
Solution 1

Solution 2

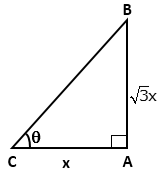
Solution 3

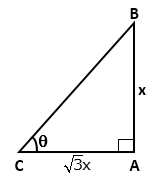
Solution 4

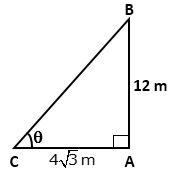
Solution 5

Solution 6

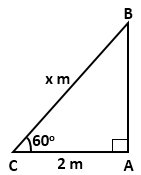
Solution 7

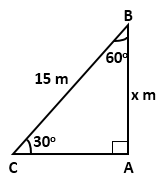
Solution 8

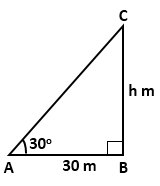
Solution 9

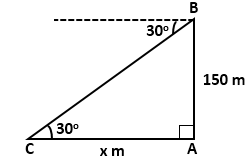
Solution 10

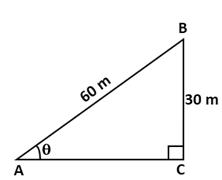
Solution 11
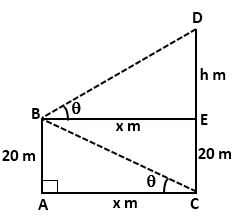

Solution 12

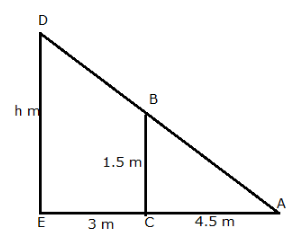
Solution 13

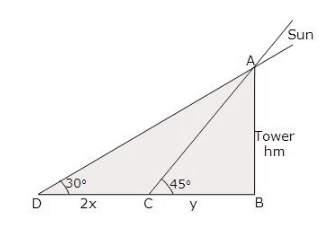
Solution 14

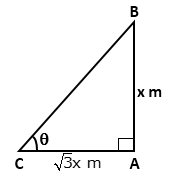
Solution 15

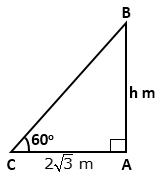
Solution 16

Solution 17

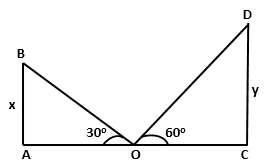
Solution 18


Solution 19

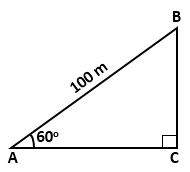
Solution 20

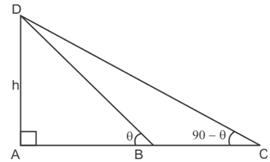
Solution 21

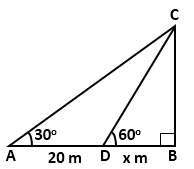
Solution 22

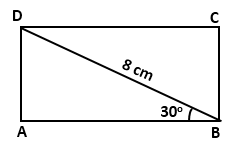
Solution 23

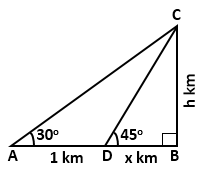
Solution 24
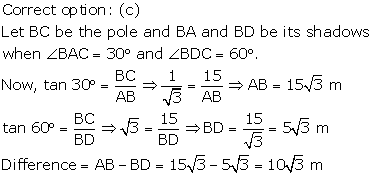
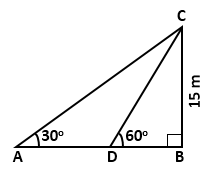
Solution 25